
杰出企业家的处事哲学总是备受关注,被大家拿出来反复研究学习,其中出现频率很高的一条,是企业家往往具备分辨并专注于做当下最重要的事情的能力。实际上对我们来说,受到经验值、拥有的信息量不足的限制,甚至在个人喜好的维度上,我们很难对诸多事情的重要性时刻做一个客观的排序,那我们不妨用另一种近似的原则对它进行替代,就是尽量去做那些有正期望值的事情。
什么是期望值?
在概率学中,期望值是一个离散性随机变量试验中,每次可能结果的概率(pk)乘以其结果(xk)的总和。理论上当观测的次数趋于无穷大的时候,每一次观测结果的平均值也就是它的期望值。
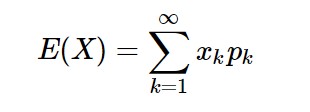
期望的应用离我们并不遥远,我们在面对每一次选择的时候,其实都有意或无意地在心中计算一下它的期望值以辅助决定,简单来说就是权衡得失和发生的可能性的结果,来判断这个选择能否预期带来收益,也就是是否为正期望值的事情。
在德州扑克的比赛转播中,会随着比赛进程向观众实时展示选手手中的牌获胜的概率,这也会是选手思考的内容的一部分。在此基础上,选手还需要综合考虑筹码情况以及对手加注或弃牌的概率等因素,做出期望值为正的决策。期望值为正并不等于当局比赛的结果即如选手预期,甚至选手心算后做出的决定会使其输掉当局比赛的筹码,现场随机抽取一名观众来做选择反而能够获得这次胜利。但长期来看,“常胜将军”还是那些坚持正期望打法的选手。
所谓正期望值,指的是当你持续做出足够多正期望值的行为时,是能够累积可观的盈利的,其中并不一定是每一次都能够获利。正期望并不是百分之百的获利保证,甚至按次数去统计的话,也不一定是胜多负少的,但按结果加和去统计的话,一定是赢大于亏的。

正的期望值等于对的结果么?
正如我们前面所阐述的,期望值是累积多次行为后得到的均值,但回溯到每一个个体上,绝大部分情况下它们并不会是均匀分布在期望值周围的。也正因如此,在期望值和单次结果之间存在着四种可能:做出正期望值的事情且得到正向反馈、做出正期望值的事情而得到负面的结果、做出负期望值的事情却得到正向反馈、做出负期望值的事情并得到负面的结果。
正期望对应正反馈是我们最愿意看到的情况,由此我们会形成一个不断自我强化的系统,负期望对应负面结果其实也并不完全是件坏事,有助于我们正视问题,然后加速脱离越努力越糟糕的困境。某种程度上来说,以上这两种情况都可以说是对的结果,但这里我们想要着重探讨的,是正期望对应负面结果和负期望对应正向反馈这两种错位的情况。

正期望的决策对应负面的结果无疑是痛苦的事情,但也是我们时常会遇到的情况,尤其当负期望的决策出现正反馈也同时出现的时候,更容易使人的意志产生动摇。这时我们不妨回溯到期望的定义上。我们需要明确的是,之所以选择去做正期望值的事情,是希望通过持续累积得到一个令人满意的结果,而并不是挂钩于某一次或者某几次的结果。
我们无法拥有“先见之明”,无法只得到期望值以上的部分而避开那些期望值以下的部分。短期看不到回报,事与愿违是再正常不过的事情,正像另一个方向上的极值也可能在意想不到的时候到来一样。
在观赏体育比赛,尤其是竞技体育的时候,不时能看到一些运动员下意识的“神来之笔”,它可能并非是遵循教练的战术安排的反应,而是当训练重复了成千上万次之后,自然而然肌肉形成了一定的条件反射,也就是我们通常所说的“肌肉记忆”。这不仅应用在体育领域,在任何一个领域,我们持续去做的事情也都是在积累肌肉记忆的过程。肌肉记忆的特点是一旦形成,动作无论是对的还是错的,改变起来都非常困难,也就是如果你重复的动作是错误的话,便会出现越努力越糟糕的情况。由此也就延伸出了我们要讨论的第四种情况,当负期望值的行为出现了正反馈。

以最典型的买彩票举个例子,假设每种可能中奖的数字或者数字组合的中奖几率是均等的,将购买成本考虑在内后,彩票就是一场期望值为负的游戏(如果期望值为正,那么意味着买入每种可能出现的结果便可确保获利),之所以参与者依旧甚多,因为头奖总是充满吸引力的,并且获得头奖并非不可能发生的事情,总会有幸运儿诞生。
负期望属性的行为并不难识别,依据常识就能够分辨,往往是那些不需要付出相应的努力或者代价,凭借触发小概率事件去搏一个存在概率的超额结果。在对负期望有充分认知情况下的参与当然也无可厚非,但如果因为某次偶然触发了正反馈而试图将其推而广之,使之成为常态,可以预见的结果就是事与愿违,并且过程中也是在加深错误的肌肉记忆。长此以往累积的结果,也只是越来越趋近负的期望值。

如何向正期望的结果靠拢?
虽然对于正期望值的行为来说,其分布列将以何种顺序呈现也是无法预知的,但总也有些什么是我们在主观层面上可以去做的。
首先,明确大概率获益和期望值为正,两者并非相等的关系。期望公式中有概率的部分,同时也要考虑每种概率下对应的结果。如果一件事情90%的概率获利10,而10%的概率损失20,这便是一件大概率获益但负期望的事情。在做出决策前除了考虑自己把握有多大以外,还要考虑如果出现负值的结果是否是自己能够承受的,以及是否愿意为了那个大概率的结果而冒此风险。正期望值对于单次行为的结果来说意义不大,想要正期望值发挥它的效力,产生累积的效果,前提是要在“游戏”中留的足够久。
其次,在过程中允许负值的出现。我们几乎不会遇到万无一失的机会,我们虽然引用墨菲定律来自嘲,越是害怕会发生什么,就越是会发生什么,但实际上只要一件事情有发生的可能,不论好坏,当重复次数足够多时,便一定会发生。有高于期望值的,就必然会有低于期望值的,甚至是负值的情况。

如前文所述,除非构成期望计算公式中的每个x值都是均等的,否则一个期望值一侧的结果也必然会在对侧至少有一个值。对于短期不如意的过分看重,纠结于如何剔除掉公式中的负值的部分甚至推翻公式,而无法聚焦于将正期望值的决定贯彻执行,会造成期望值的偏离。初衷虽好,但对长期结果往往反而是负贡献的。没有人可以只摘取大于期望值的那部分结果的,因为如果这种行为成立了,这个新的分布列又将会对应一个更高的期望值。
由此我想不妨在开头传统的期望公式中加一个变量,得到一个期望公式的2.0版本:
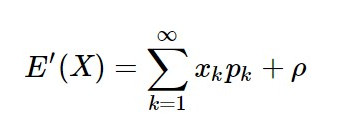
2.0版本的公式的基本含义和原始的期望公式没有差异,而新增的变量ρ,即对每个人来说,都能够发挥主观能动性去赋予期望值的一部分,它可能是正值也可能是负值,取决于每个人自身的作为。在面对同样的事情时,无论好事还是坏事,不同的人会做出不同的反应,有的人会任由其发生过去,有的人因为负值出现灰心丧气发生漂移,有的人会总结提炼经验为未来所用,而对每个人来说,同一件事情的期望值也在这个过程中悄然发生变化。
我们是无法针对构成每一个正期望行为的每一种可能性都定制一个应对方案的,但在我们能够掌握的部分上赋一个正值,把底线整体垫高,以避免出现向下无法接受的极值,同时又能在向上的过程中叠加锦上添花的效果,正期望值也得以拔高。

写在最后:
“取乎其上,得乎其中;取乎其中,得乎其下;取乎其下,则无所得矣。”我们虽无法左右正期望值的行为以怎样具体的形态分布,但个人主观因素的影响因子仍是每个人自己能够把握并且为之努力的,而这也会是理论期望值和最终实际值的偏差所在。
声明:
投资有风险,本文的观点论述及观点分享仅出于传播信息的需要。内容仅供参考,不构成任何投资建议。
本文章版权为北京汉和汉华资本管理有限公司所有,任何媒体、网站或个人未经本公司授权不得以转载、链接、转贴或以其他方式复制发布/发表。已经本公司授权的媒体、网站或个人在引用时需注明出处为“汉和资本”,且不得对本文进行有悖原意的引用、删节和修改。本公司保留追究法律责任的权利。












